1.创设情境
尺规作图就是用无刻度的直尺和圆规来作图,起源于古希腊
希腊人强调作图只能用直尺圆规,有下列原因:
①希腊几何的基本精神,是从极少的基本假定(定义、公理、公设)出发,推导出尽可能多的命题。
②以毕达哥拉斯学派为代表的希腊人认为圆是最完美的平面图形,圆和直线是几何学最基本的研究对象。史上最早明确提出尺规限制的是伊诺皮迪斯,他发现以下作图法:在已知直线的已知点上作一角与已知角相等。伊诺皮迪斯以后,尺规的限制逐渐成为一种公约,最后总结在《几何原本》之中。
如果能够使用尽量少的条件,作出与已知三角形全等的三角形,那么这些条件既可以作为三角形全等的判定定理。
三角形含有三条边、三个内角,六个几何要素。
使用的条件尽量少,证明方法越简单。我们可以按满足“一个条件、两个条件、三个条件……”开始研究。
问1:当满足一个条件时,△ABC 与△A'B'C'全等吗?
需要再分两种情况进行说明,即一条边分别相等、一个角分别相等,在探究过程中,可以通过画图加以说明,也可以利用三角尺等进行说明.
注:依靠一个条件,无法作出全等三角形,让学生在作图时,体会所作三角形不唯一,所以不能作为三角形全等的判定定理。
问2:当满足两个条件时,△ABC 与△A'B'C'全等吗?
学生独立思考:满足“两个条件”分两边、一边一角或两角分别相等三种情况。学生分三组分别进行探究,通过画图、展示交流,最后得出结论:只满足“两个条件”的两个三角形不一定全等.
注:(1)依靠二组角对应相等,能够作出无数个相似三角形,只能保证形状相同,大小无法保证相等;
(2)两组边对应相等,一边通过作图,可以作出无数个三角形,另一方面三边关系定理,可以知道:|a-b|<c<a+b,第三边存在无数条;
(3)一组边一组角对应相等,通过作图实践,第三组边存在无数条。
所以通过两个条件,无法作出全等三角形,让学生在作图时,体会所作三角形不唯一,所以不能作为三角形全等的判定定理。
问3:当满足三个条件时,△ABC 与△A'B'C'全等吗?满足三个条件时,又分为几种情况呢?
学生回答问题,并相互补充,发现需要分四种情况进行研究,即三边、三角、两边一角、两角一边分别相等.
通过尺规作图探究三角形全等的判定定理,首先教给学生研究数学的一般方法,由简到繁,分类进行,逐层深入,等到一般结论。其次激励学生充分参与到探究过程中,层层深入地思考问题,培养动手能力,加深对三角形判定定理的认识。
2.尺规基本作图:
(1)作一条线段与已知线段相等

作等线段方法
(2)作一个角与已知角相等
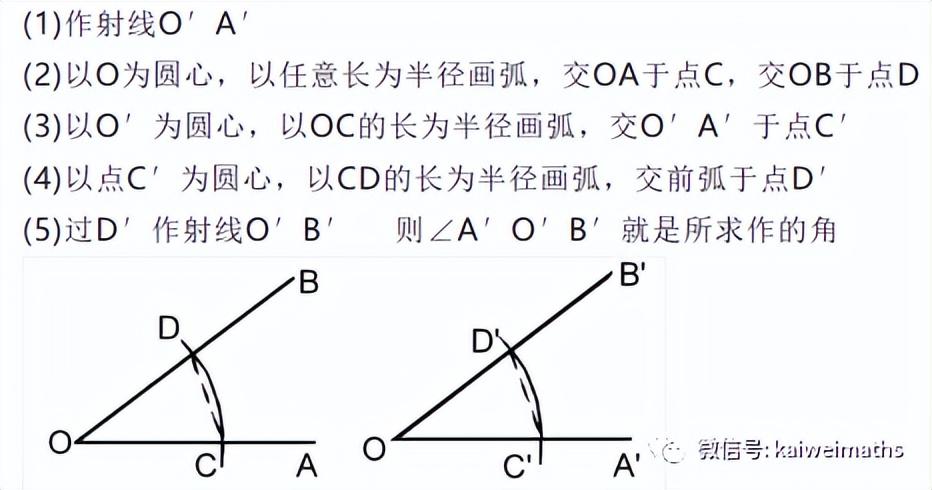
作等角方法
这两个基本作图,学生以前没有经验,教师尺规作图做示范。
3.尺规作图,探究“边边边”判定方法
尺规作图:已知△ABC,画一个△A'B'C',使AB=A'B',AC=A'C',BC=B'C'.
并判断△ABC和△A'B'C'是否全等.

全等三角形判定定理SSS
通过对于条件由少到多的分析,满足三个条件,终于找到三角形全等的判定定理。作图过程尽量交给学生完成,探究过程使学生收获成就感。
通过作图探究,总结得到全等三角形判定定理——SSS,给出明确定理表述。

应用三角形全等判定定理前,先教受三角形全等证明书写格式。如下图
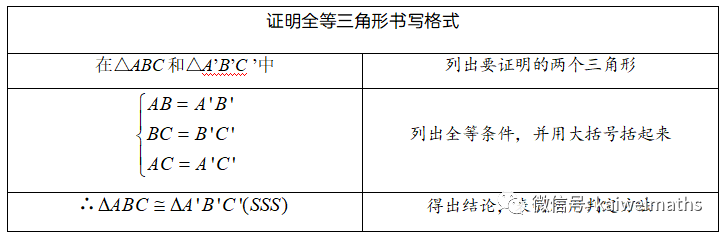
强调对应顶点写在对应位置上;罗列条件时,按照判定定理的边角位置,进行书写;得到全等后,应该书写判定定理类型。
注意:寻找全等三角形的对应角,对应边的一般规律是:
⑴把其中一个图形通过平移、翻折或旋转,能与另一个图形完全重合,则重合的边就是对应边,重合的角就是对应角,表示两个三角形全等时,要把对应字母写在对应位置上.
⑵有公共边时,则公共边为对应边;有公共角时,则公共角为对应角(对顶角为对应角);最大边与最大边(最小边与最小边)为对应边;最大角与最大角(最小角与最小角)为对应角.

例4设计目的一方面在平移变换中,训练全等三角形判定定理SSS的应用,另一方面培养学生分析问题和规范全等证明书写格式,要求推理步步有据。
4.尺规作图,探究“边角边”判定方法
尺规作图:已知△ABC,画一个△A'B'C',使AB=A'B',AC=A'C',∠A=∠A'.
并判断△ABC和△A'B'C'是否全等.

全等三角形判定定理SAS
此判定定理重点是作相等角,难点是对于作图的唯一情况的认识和理解。
设计好作图流程,探究过程交给学生独立完成,教师可以指导学生作图,并且把符合作图要求的同学作法在黑板上再展示一遍,强化大家对于定理的理解。
同上,通过作图探究,总结得到全等三角形判定定理——SAS,给出明确定理表述。


例5设计目的是通过旋转变换,呈现全等三角形,其中注意角度等量关系的推理,并且与例4中线段的等量关系类比分析,进一步抽象等量间的关系推理,本质一致性。本例题即训练判定定理SAS,也培养学生养成良好的推理能力和书写规范。
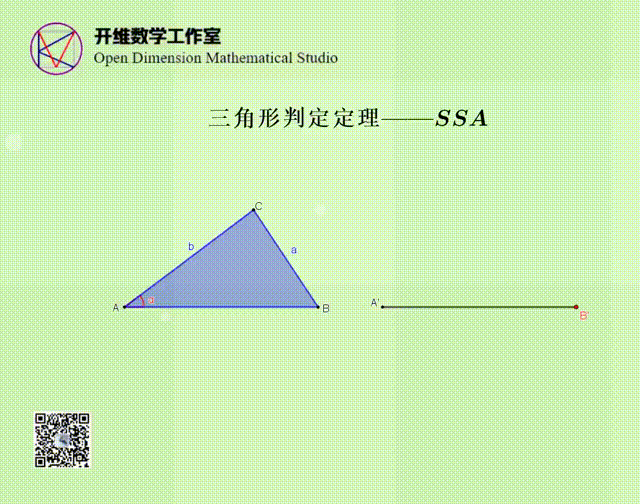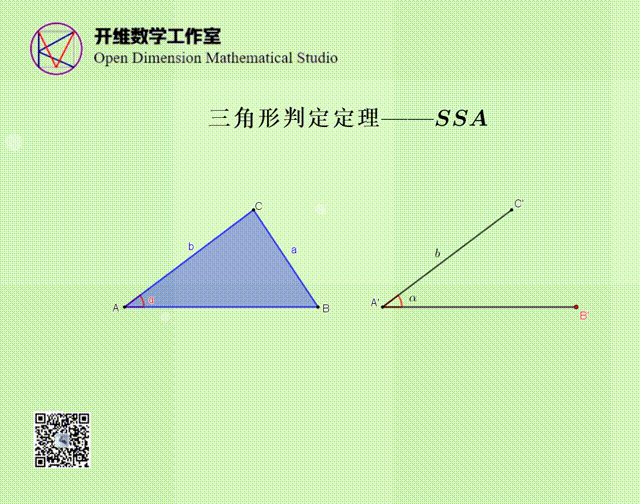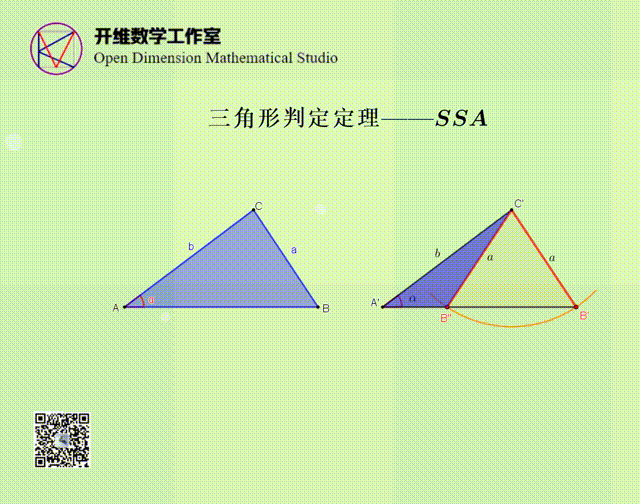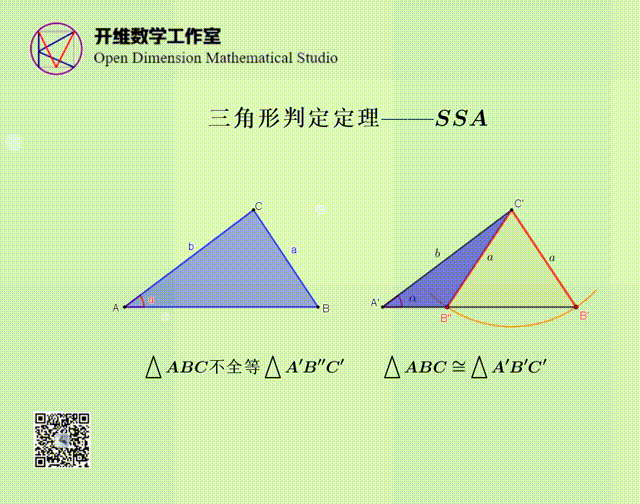
SSA不能作为判定定理的原因
通过动画演示,说明SSA的条件可以作出两个三角形,其中一个与△ABC不全等,所以SSA不能作为全等三角形的判定定理。
总结:
1.通过画三角形的探究活动,归纳出确定三角形的形状、大小至少需要三个元素,并能进行分类,如“边边边、边角边、”,通过画图,概括出基本事实“两边及其夹角分别相等的两个三角形全等”,“三边分别相等的两个三角形全等”。
2.通过画图,推断符合“角角角、边边角”条件的两个三角形不一定全等。
3.能利用三角形全等的判定方法证明两个三角形全等,在分析证明思路和书写证明过程中帮助学生形成有理有据的逻辑推理能力。
